Křivka
Z Multimediaexpo.cz
m (Nahrazení textu „<math>“ textem „<big>\(“) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| Řádka 2: | Řádka 2: | ||
'''Křivka''' je v [[matematika|matematice]] [[geometrie|geometrický]] jednorozměrný objekt, případně zobrazení z [[úsečka|úsečky]] do nějakého matematického prostoru (tzv. parametrizovaná křivka). Jednoduchý příklad křivky je například [[kružnice]] nebo [[přímka]]. | '''Křivka''' je v [[matematika|matematice]] [[geometrie|geometrický]] jednorozměrný objekt, případně zobrazení z [[úsečka|úsečky]] do nějakého matematického prostoru (tzv. parametrizovaná křivka). Jednoduchý příklad křivky je například [[kružnice]] nebo [[přímka]]. | ||
== Formální definice == | == Formální definice == | ||
| - | Je-li ''M'' nějaký matematický prostor (například [[Eukleidovský prostor]], [[varieta (matematika)|varieta]], [[topologický prostor]]) a ''I'' [[Interval (matematika)|interval]] reálných čísel, pak křivkou <big>\(k</ | + | Je-li ''M'' nějaký matematický prostor (například [[Eukleidovský prostor]], [[varieta (matematika)|varieta]], [[topologický prostor]]) a ''I'' [[Interval (matematika)|interval]] reálných čísel, pak křivkou <big>\(k\)</big> rozumíme [[spojitost|spojité]] [[zobrazení (matematika)|zobrazení]] z ''I'' do ''M''. Toto se někdy také nazývá '''parametrická křivka'''. Pokud má smysl mluvit o [[derivace|derivaci]] ''k'' (t.j. pokud cílový prostor je [[Euklidův prostor]] nebo [[varieta (matematika)|hladká varieta]] a derivace existuje v každém bodě), nazývá se křivka '''hladká''', anebo '''diferenciální'''. Hladká křivka je '''regulární''', pokud její derivace není v žádném bodě nulová. Křivka se nazývá '''uzavřená''', pokud ''I'' je uzavřený interval ''[a,b]'' a <big>\(k(a)=k(b)\)</big>. Množina <big>\(\{k(x);\,x\in I\}\)</big> se nazývá '''obraz křivky'''. Mají-li složky <big>\(k_i\)</big> křivky ''k'' na otevřeném [[interval (matematika)|intervalu]] <big>\((a,b)\)</big> spojité derivace až do <big>\(r\)</big>-tého řádu, pak říkáme, že se jedná o ''křivku <big>\(r\)</big>-té třídy''. Má-li křivka všechny derivace, říkáme někdy, že je třídy nekonečno, nebo-li někonečně diferencovatelná. |
Někdy se slovem ''křivka'' myslí jenom obraz křivky (v dřívější definici), t.j. množina bodů. Toto se někdy také nazývá '''neparametrická křivka'''. | Někdy se slovem ''křivka'' myslí jenom obraz křivky (v dřívější definici), t.j. množina bodů. Toto se někdy také nazývá '''neparametrická křivka'''. | ||
== Rovinná křivka == | == Rovinná křivka == | ||
'''Rovinnou křivkou''' rozumíme [[zobrazení (matematika)|zobrazení]] | '''Rovinnou křivkou''' rozumíme [[zobrazení (matematika)|zobrazení]] | ||
| - | :<big>\(x = \phi(t)</ | + | :<big>\(x = \phi(t)\)</big> |
| - | :<big>\(y = \psi(t)</ | + | :<big>\(y = \psi(t)\)</big> |
| - | pro <big>\(t \in \langle\alpha,\beta\rangle</ | + | pro <big>\(t \in \langle\alpha,\beta\rangle\)</big>, kde <big>\(\phi\)</big> a <big>\(\psi\)</big> jsou spojité funkce. |
| - | Předpokládáme obvykle, že [[funkce (matematika)|funkce]] <big>\(\phi(t), \psi(t)</ | + | Předpokládáme obvykle, že [[funkce (matematika)|funkce]] <big>\(\phi(t), \psi(t)\)</big> jsou na [[interval (matematika)|intervalu]] <big>\(\langle\alpha,\beta\rangle\)</big> [[spojitá funkce|spojité]] a mají na tomto intervalu po částech spojité [[derivace]] <big>\(\phi^\prime(t), \psi^\prime(t)\)</big>. Někdy se předpokládá, že funkce <big>\(\phi, \psi\)</big> jsou pouze spojité, pak se ale může stát že obraz křivky je celý dvourozměrný čtverec. |
| - | Křivku nazveme ''regulární'', pokud pro žádné <big>\(t</ | + | Křivku nazveme ''regulární'', pokud pro žádné <big>\(t\)</big> nejsou derivace <big>\(\phi^\prime(t), \psi^\prime(t)\)</big> současně [[nula|nulové]]. Křivku, která neprotíná sama sebe (t.j. je prostá) označujeme jako '''jednoduchou'''. |
| - | Rovnici obrazu rovinné křivky lze často vyjádřit ve formě funkční závislosti [[proměnná|proměnných]] <big>\(x, y</ | + | Rovnici obrazu rovinné křivky lze často vyjádřit ve formě funkční závislosti [[proměnná|proměnných]] <big>\(x, y\)</big>, tzn. |
| - | :<big>\(y=f(x)</ | + | :<big>\(y=f(x)\)</big>, |
popř. | popř. | ||
| - | :<big>\(F(x,y)=0</ | + | :<big>\(F(x,y)=0\)</big>. |
| - | Pokud platí současně <big>\(\phi(\alpha)=\phi(\beta), \psi(\alpha)=\psi(\beta)</ | + | Pokud platí současně <big>\(\phi(\alpha)=\phi(\beta), \psi(\alpha)=\psi(\beta)\)</big>, tzn. počáteční bod křivky splývá s bodem koncovým, pak křivku označíme jako '''uzavřenou'''. |
Křivku označíme jako '''rektifikovatelnou''', pokud má konečnou [[délka|délku]], kterou lze vyjádřit jako | Křivku označíme jako '''rektifikovatelnou''', pokud má konečnou [[délka|délku]], kterou lze vyjádřit jako | ||
| - | :<big>\(l = \int_\alpha^\beta \sqrt{{\phi^\prime}^2(t)+{\psi^\prime}^2(t)}\mathrm{d}t</ | + | :<big>\(l = \int_\alpha^\beta \sqrt{{\phi^\prime}^2(t)+{\psi^\prime}^2(t)}\mathrm{d}t\)</big> |
| - | Někdy se také slovem křivka myslí '''množina''' bodů <big>\(\{(\phi(t), \psi(t));\, t\in<\alpha,\beta>\}</ | + | Někdy se také slovem křivka myslí '''množina''' bodů <big>\(\{(\phi(t), \psi(t));\, t\in<\alpha,\beta>\}\)</big>. |
=== Jordanova křivka === | === Jordanova křivka === | ||
Jednoduchou rektifikovatelnou uzavřenou křivku (která nemusí být po částech hladká) označujeme jako '''Jordanovu křivku'''. Jordanova křivka je uzavřená, takže rozděluje rovinu na dvě souvislé oblasti. Tu, která je [[Omezená množina|omezená]] označujeme jako '''vnitřek křivky''' (nebo '''Jordanovu oblast'''), zbytek roviny pak jako '''vnějšek křivky'''. | Jednoduchou rektifikovatelnou uzavřenou křivku (která nemusí být po částech hladká) označujeme jako '''Jordanovu křivku'''. Jordanova křivka je uzavřená, takže rozděluje rovinu na dvě souvislé oblasti. Tu, která je [[Omezená množina|omezená]] označujeme jako '''vnitřek křivky''' (nebo '''Jordanovu oblast'''), zbytek roviny pak jako '''vnějšek křivky'''. | ||
=== Orientace křivky === | === Orientace křivky === | ||
| - | Na neparametrické hladké křivce (t.j. množině, která je obrazem parametrické hladké křivky) můžme zvolit dvě [[orientace]], což je volba směru, kterým se křivka pohybuje. Formálněji, je to volba baze jejího (jednorozměrného) tečného prostoru v každém bodě. Tvoří-li uzavřená křivka hranici určité oblasti <big>\(\Omega</ | + | Na neparametrické hladké křivce (t.j. množině, která je obrazem parametrické hladké křivky) můžme zvolit dvě [[orientace]], což je volba směru, kterým se křivka pohybuje. Formálněji, je to volba baze jejího (jednorozměrného) tečného prostoru v každém bodě. Tvoří-li uzavřená křivka hranici určité oblasti <big>\(\Omega\)</big>, pak řekneme, že je ''kladně orientovaná'' vzhledem k <big>\(\Omega\)</big>, pokud oblast <big>\(\Omega\)</big> zůstává po levé straně křivky (při pohybu po kladně orientované křivce jde o pohyb proti směru hodinových ručiček). Formálněji, křivka je kladně orientována, pokud normálový vektor k oblasti <big>\(\Omega\)</big> a tečný vektor ke křivce určen její orientací tvoří kladnou bázi tečného prostoru (souřadnice těchto vektorů napsány ve sloupcích vedle sebe tvoří [[matice|matici]], která má kladný [[determinant]]). V opačném případě se jedná o ''záporně orientovanou křivku''. |
=== Příklady rovinných křivek === | === Příklady rovinných křivek === | ||
* [[přímka]] ležící v zadané [[rovina|rovině]] | * [[přímka]] ležící v zadané [[rovina|rovině]] | ||
| Řádka 31: | Řádka 31: | ||
== Prostorová křivka == | == Prostorová křivka == | ||
'''Prostorovou křivkou''' rozumíme [[zobrazení (matematika)|zobrazení]] | '''Prostorovou křivkou''' rozumíme [[zobrazení (matematika)|zobrazení]] | ||
| - | :<big>\(x = x(t)</ | + | :<big>\(x = x(t)\)</big> |
| - | :<big>\(y = y(t)</ | + | :<big>\(y = y(t)\)</big> |
| - | :<big>\(z = z(t)</ | + | :<big>\(z = z(t)\)</big> |
| - | pro <big>\(t \in \langle\alpha,\beta\rangle</ | + | pro <big>\(t \in \langle\alpha,\beta\rangle\)</big>, kde ''x'', ''y'' a ''z'' jsou spojité funkce. |
Uvedené rovnice křivky bývají obvykle zapisovány ve [[vektor]]ovém tvaru | Uvedené rovnice křivky bývají obvykle zapisovány ve [[vektor]]ovém tvaru | ||
| - | :<big>\(\mathbf{r} = \mathbf{r}(t)</ | + | :<big>\(\mathbf{r} = \mathbf{r}(t)\)</big>, |
| - | kde <big>\(\mathbf{r}</ | + | kde <big>\(\mathbf{r}\)</big> představuje [[rádiusvektor]]. |
Křivku v prostoru lze také zadat jako [[průnik]] dvou [[plocha|ploch]], např. | Křivku v prostoru lze také zadat jako [[průnik]] dvou [[plocha|ploch]], např. | ||
| - | :<big>\(z=f(x,y)</ | + | :<big>\(z=f(x,y)\)</big> |
| - | :<big>\(z=g(x,y)</ | + | :<big>\(z=g(x,y)\)</big> |
nebo | nebo | ||
| - | :<big>\(F(x,y,z)=0</ | + | :<big>\(F(x,y,z)=0\)</big> |
| - | :<big>\(G(x,y,z)=0.</ | + | :<big>\(G(x,y,z)=0.\)</big> |
Jsou-li rovnice popisující křivku [[algebraická rovnice|algebraické]], pak křivku označujeme jako '''algebraickou'''. Pokud uvedené rovnice nejsou algebraické, pak říkáme, že křivka je '''transcendentní'''. | Jsou-li rovnice popisující křivku [[algebraická rovnice|algebraické]], pak křivku označujeme jako '''algebraickou'''. Pokud uvedené rovnice nejsou algebraické, pak říkáme, že křivka je '''transcendentní'''. | ||
| - | Někdy se také slovem křivka myslí '''množina''' bodů <big>\(\{(x(t), y(t), z(t));\, t\in<\alpha,\beta>\}</ | + | Někdy se také slovem křivka myslí '''množina''' bodů <big>\(\{(x(t), y(t), z(t));\, t\in<\alpha,\beta>\}\)</big>. |
=== Příklady prostorových křivek === | === Příklady prostorových křivek === | ||
* [[přímka]] | * [[přímka]] | ||
* [[šroubovice]] | * [[šroubovice]] | ||
== Oblouk křivky == | == Oblouk křivky == | ||
| - | '''Obloukem křivky''' <big>\(k: [a,b]\to \R^n</ | + | '''Obloukem křivky''' <big>\(k: [a,b]\to \R^n\)</big> od bodu <big>\(t_0 \in \langle a,b\rangle\)</big> do bodu <big>\(t \in \langle a,b\rangle\)</big> se nazývá ''délka'' části křivky mezi ''k(t_0)'' a k(t). Pokud je křivka diferencovatelná (t.j. ''k'' má derivace), dá se spočíst vzorcem |
| - | :<big>\(s = \int_{t_0}^t \sqrt{{\sum_i \left(\frac{\mathrm{d}k_i}{\mathrm{d}t}\right)}^2} \mathrm{d} t</ | + | :<big>\(s = \int_{t_0}^t \sqrt{{\sum_i \left(\frac{\mathrm{d}k_i}{\mathrm{d}t}\right)}^2} \mathrm{d} t\)</big> |
| - | kde <big>\(k_i</ | + | kde <big>\(k_i\)</big> je ''i''-tá složka křivky. |
[[Diferenciál (matematika)|Diferenciál]] | [[Diferenciál (matematika)|Diferenciál]] | ||
| - | :<big>\(\mathrm{d}s = \sqrt{\frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t}\cdot\frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t}}\mathrm{d}t = \sqrt{\mathrm{d}\mathbf{r}\cdot\mathrm{d}\mathbf{r}} = \sqrt{\sum_i\mathrm{d}k_i^2}</ | + | :<big>\(\mathrm{d}s = \sqrt{\frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t}\cdot\frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t}}\mathrm{d}t = \sqrt{\mathrm{d}\mathbf{r}\cdot\mathrm{d}\mathbf{r}} = \sqrt{\sum_i\mathrm{d}k_i^2}\)</big> |
nazýváme ''diferenciál (prvek, element) oblouku'' nebo ''lineární prvek (element) křivky''. | nazýváme ''diferenciál (prvek, element) oblouku'' nebo ''lineární prvek (element) křivky''. | ||
== Křivky vyplňující prostor == | == Křivky vyplňující prostor == | ||
Aktuální verze z 14. 8. 2022, 14:52
Křivka je v matematice geometrický jednorozměrný objekt, případně zobrazení z úsečky do nějakého matematického prostoru (tzv. parametrizovaná křivka). Jednoduchý příklad křivky je například kružnice nebo přímka.
Obsah |
Formální definice
Je-li M nějaký matematický prostor (například Eukleidovský prostor, varieta, topologický prostor) a I interval reálných čísel, pak křivkou \(k\) rozumíme spojité zobrazení z I do M. Toto se někdy také nazývá parametrická křivka. Pokud má smysl mluvit o derivaci k (t.j. pokud cílový prostor je Euklidův prostor nebo hladká varieta a derivace existuje v každém bodě), nazývá se křivka hladká, anebo diferenciální. Hladká křivka je regulární, pokud její derivace není v žádném bodě nulová. Křivka se nazývá uzavřená, pokud I je uzavřený interval [a,b] a \(k(a)=k(b)\). Množina \(\{k(x);\,x\in I\}\) se nazývá obraz křivky. Mají-li složky \(k_i\) křivky k na otevřeném intervalu \((a,b)\) spojité derivace až do \(r\)-tého řádu, pak říkáme, že se jedná o křivku \(r\)-té třídy. Má-li křivka všechny derivace, říkáme někdy, že je třídy nekonečno, nebo-li někonečně diferencovatelná. Někdy se slovem křivka myslí jenom obraz křivky (v dřívější definici), t.j. množina bodů. Toto se někdy také nazývá neparametrická křivka.
Rovinná křivka
Rovinnou křivkou rozumíme zobrazení
- \(x = \phi(t)\)
- \(y = \psi(t)\)
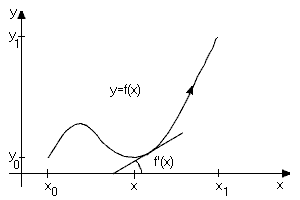
pro \(t \in \langle\alpha,\beta\rangle\), kde \(\phi\) a \(\psi\) jsou spojité funkce. Předpokládáme obvykle, že funkce \(\phi(t), \psi(t)\) jsou na intervalu \(\langle\alpha,\beta\rangle\) spojité a mají na tomto intervalu po částech spojité derivace \(\phi^\prime(t), \psi^\prime(t)\). Někdy se předpokládá, že funkce \(\phi, \psi\) jsou pouze spojité, pak se ale může stát že obraz křivky je celý dvourozměrný čtverec. Křivku nazveme regulární, pokud pro žádné \(t\) nejsou derivace \(\phi^\prime(t), \psi^\prime(t)\) současně nulové. Křivku, která neprotíná sama sebe (t.j. je prostá) označujeme jako jednoduchou. Rovnici obrazu rovinné křivky lze často vyjádřit ve formě funkční závislosti proměnných \(x, y\), tzn.
- \(y=f(x)\),
popř.
- \(F(x,y)=0\).
Pokud platí současně \(\phi(\alpha)=\phi(\beta), \psi(\alpha)=\psi(\beta)\), tzn. počáteční bod křivky splývá s bodem koncovým, pak křivku označíme jako uzavřenou. Křivku označíme jako rektifikovatelnou, pokud má konečnou délku, kterou lze vyjádřit jako
- \(l = \int_\alpha^\beta \sqrt{{\phi^\prime}^2(t)+{\psi^\prime}^2(t)}\mathrm{d}t\)
Někdy se také slovem křivka myslí množina bodů \(\{(\phi(t), \psi(t));\, t\in<\alpha,\beta>\}\).
Jordanova křivka
Jednoduchou rektifikovatelnou uzavřenou křivku (která nemusí být po částech hladká) označujeme jako Jordanovu křivku. Jordanova křivka je uzavřená, takže rozděluje rovinu na dvě souvislé oblasti. Tu, která je omezená označujeme jako vnitřek křivky (nebo Jordanovu oblast), zbytek roviny pak jako vnějšek křivky.
Orientace křivky
Na neparametrické hladké křivce (t.j. množině, která je obrazem parametrické hladké křivky) můžme zvolit dvě orientace, což je volba směru, kterým se křivka pohybuje. Formálněji, je to volba baze jejího (jednorozměrného) tečného prostoru v každém bodě. Tvoří-li uzavřená křivka hranici určité oblasti \(\Omega\), pak řekneme, že je kladně orientovaná vzhledem k \(\Omega\), pokud oblast \(\Omega\) zůstává po levé straně křivky (při pohybu po kladně orientované křivce jde o pohyb proti směru hodinových ručiček). Formálněji, křivka je kladně orientována, pokud normálový vektor k oblasti \(\Omega\) a tečný vektor ke křivce určen její orientací tvoří kladnou bázi tečného prostoru (souřadnice těchto vektorů napsány ve sloupcích vedle sebe tvoří matici, která má kladný determinant). V opačném případě se jedná o záporně orientovanou křivku.
Příklady rovinných křivek
Prostorová křivka
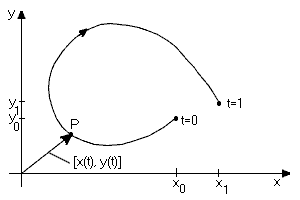
Prostorovou křivkou rozumíme zobrazení
- \(x = x(t)\)
- \(y = y(t)\)
- \(z = z(t)\)
pro \(t \in \langle\alpha,\beta\rangle\), kde x, y a z jsou spojité funkce. Uvedené rovnice křivky bývají obvykle zapisovány ve vektorovém tvaru
- \(\mathbf{r} = \mathbf{r}(t)\),
kde \(\mathbf{r}\) představuje rádiusvektor. Křivku v prostoru lze také zadat jako průnik dvou ploch, např.
- \(z=f(x,y)\)
- \(z=g(x,y)\)
nebo
- \(F(x,y,z)=0\)
- \(G(x,y,z)=0.\)
Jsou-li rovnice popisující křivku algebraické, pak křivku označujeme jako algebraickou. Pokud uvedené rovnice nejsou algebraické, pak říkáme, že křivka je transcendentní. Někdy se také slovem křivka myslí množina bodů \(\{(x(t), y(t), z(t));\, t\in<\alpha,\beta>\}\).
Příklady prostorových křivek
Oblouk křivky
Obloukem křivky \(k: [a,b]\to \R^n\) od bodu \(t_0 \in \langle a,b\rangle\) do bodu \(t \in \langle a,b\rangle\) se nazývá délka části křivky mezi k(t_0) a k(t). Pokud je křivka diferencovatelná (t.j. k má derivace), dá se spočíst vzorcem
- \(s = \int_{t_0}^t \sqrt{{\sum_i \left(\frac{\mathrm{d}k_i}{\mathrm{d}t}\right)}^2} \mathrm{d} t\)
kde \(k_i\) je i-tá složka křivky. Diferenciál
- \(\mathrm{d}s = \sqrt{\frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t}\cdot\frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t}}\mathrm{d}t = \sqrt{\mathrm{d}\mathbf{r}\cdot\mathrm{d}\mathbf{r}} = \sqrt{\sum_i\mathrm{d}k_i^2}\)
nazýváme diferenciál (prvek, element) oblouku nebo lineární prvek (element) křivky.
Křivky vyplňující prostor
Obrazem křivky můžou být i množiny, které mají větší topologickou dimenzi než jedna. Kupříkladu Hilbertova křivka je spojité zobrazení úsečky na čtverec, t.j. spojitá křivka, která vyplní celý (dvou-rozměrný) čtverec.
Na obrázku je prvních 6 iterací kontrukce Hilbertovy křivky. Hilbertova křivka je pak limitou těchto křivek. Je spojitá, ale není prostá. Její složky jsou spojité funkce, které nemají derivaci v žádném bodě. Jiný známý příklad křivky, která vyplní čtverec, je tzv. Sierpinského křivka. Klasifikace, který topologický prostor je spojitým obrazem intervalu [0,1], řeší tzv. Hahn–Mazurkiewiczova věta:
- Neprázdny hausdorfův topologický prostor X je spojitým obrazem intervalu [0,1] právě když je kompaktní, souvislý, lokálně souvislý a separabliní.
Speciálně tedy každá kompaktní souvislá varieta se dá "vyplnit" křivkou.
Příklady
Související články
- Lagrangeova interpolace
- C1 kubická interpolace
- C2 kubická interpolace
- Hermitova kubika
- Algoritmus de Casteljau
- Racionální Algoritmus de Casteljau
- Afinní transformace souřadnic
- Výpočet průsečíku křivek
Literatura
- Rektorys, K. a spol.: Přehled užité matematiky I.. Prometheus, Praha, 2003, 7. vydání. ISBN 80-7196-179-5
Externí odkazy
- Některé rovinné křivky - lemniskáta, Archimédova spirála, atd. (pdf)
- Historický vývoj pojmu křivka (disertační práce, pdf)
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |