Určitý integrál
Z Multimediaexpo.cz
m (1 revizi) |
(+ Aktualizace) |
||
| Řádka 1: | Řádka 1: | ||
| - | + | [[Soubor:UrcityIntegral.png|thumb|290px|Určitý integrál souvisí s obsahem plochy pod grafem funkce.]] | |
| + | '''Určitý integrál''' je [[Matematika|matematický]] nástroj, který umožňuje určit změnu funkce na základě informace o tom, jak rychle se funkce mění na daném intervalu. Určitý integrál nezáporné funkce má názornou geometrickou interpretaci, jedná se o obsah plochy pod grafem této funkce na uvažovaném intervalu. | ||
| + | Z formálního hlediska je vstupními údaji určitého integrálu funkce a dvě čísla (integrační meze) a výstupem je číslo (hodnota integrálu). Tím se liší od [[Neurčitý integrál|neurčitého integrálu]], který má na vstupu funkci a výstupem je [[množina]] funkcí lišících se o aditivní konstantu. | ||
| + | |||
| + | Určitý integrál má mnoho aplikací v [[Teorie pravděpodobnosti|teorii pravděpodobnosti]], [[Funkcionální analýza|funkcionální analýze]], [[Fyzika|fyzice]], např. častou fyzikální aplikací je určení dráhy tělesa ze známé rychlosti. | ||
| + | |||
| + | == Definice == | ||
| + | Existují různé definice určitého integrálu podle formulace integrálních součtů, tyto definice se liší množinou funkcí, které jsou podle nich integrovatelné (pokud je pro několik definicí funkce integrovatelná, pak je hodnota integrálu stejná), tj. existují různé určité integrály: | ||
| + | |||
| + | === Newtonův integrál === | ||
| + | {{Viz též|Newtonův integrál}} | ||
| + | Pokud je funkce <big>\(f\)</big> [[Spojitá funkce|spojitá]] na [[interval (matematika)|intervalu]] <big>\(\langle a,b\rangle\)</big> a funkce <big>\(F\)</big> je k ní na tomto intervalu [[Primitivní funkce|primitivní]], pak platí: | ||
| + | |||
| + | :<big>\(\int_a^b f(x) \ \mathrm{d}x = {[F(x)]}_a^b = F(b)-F(a)\)</big>. | ||
| + | |||
| + | === Zobecněný Newtonův integrál === | ||
| + | Newtonova definice určitého integrálu požaduje [[Spojitá funkce|spojitost]] [[funkce (matematika)|funkce]] na daném intervalu. Pokud je funkce na intervalu pouze po částech spojitá, lze interval v bodech nespojitosti rozdělit a hledat primitivní funkce po částech. Pro tento případ se definuje takzvaný „zobecněný Newtonův integrál“, který je v případě nespojitosti primitivní funkce v krajních bodech definován jako rozdíl [[jednostranná limita|jednostranných krajních limit]]: | ||
| + | |||
| + | :<big>\(\int_a^b f(x) \ \mathrm{d}x = \lim_{x\to b^-} F(x)-\lim_{x\to a^+} F(x)\)</big>. | ||
| + | |||
| + | === Riemannův integrál === | ||
| + | {{Viz též|Riemannův integrál}} | ||
| + | Řekneme, že po částech spojitá funkce <big>\(f\)</big> na intervalu <big>\(\langle a,b \rangle\)</big> má Riemannův integrál <big>\(I\)</big>, pokud pro každé <big>\(\varepsilon > 0 \)</big> existuje <big>\(\delta>0\)</big> takové, že pro každé dělení body <big>\((D,C)\)</big> intervalu <big>\(\langle a,b \rangle\)</big> platí, že: | ||
| + | |||
| + | :<big>\(\lambda(D) < \delta \,=> \,|I - R(f,D,C)| < \varepsilon\)</big>, tj. <big>\(I = \lim_{\lambda(D) \to 0}R(f,D,C) = \int\limits_{a}^{b} f(x) \ \mathrm{d}x\)</big>, | ||
| + | |||
| + | kde <big>\(R(f,D,C)\)</big> je Riemannova suma a <big>\(\lambda(D)\)</big> resp. <big>\(C\)</big> je norma dělení <big>\(D\)</big> resp. množina bodů zapouzdřených v dělení <big>\(D\)</big>. | ||
| + | |||
| + | === Lebesgueův integrál === | ||
| + | {{Viz též|Lebesgueův integrál}} | ||
| + | Na základě [[Lebesgueova míra|Lebesgueovy míry]] definoval [[Henri Lebesgue]] tzv. Lebesgueův integrál. Má podobnou definici jako [[Riemannův integrál#Definice|Darbouxova definice]] Riemannova integrálu, ale třída integrovatelných funkcí je v něm mnohem širší – dokonce se bez [[Axiom výběru|axiomu výběru]] nedá prokázat, že existuje funkce, která není Lebesgueovsky integrovatelná. Podobný postup použili i další matematici. Lebesgueův integrál a další, ještě pokročilejší integrály, umožňují integrovat širší třídy funkcí, platí pro ně silnější verze mnoha tvrzení a skýtají i mnoho jiných výhod. Patří mezi ně například [[Stieltjesův integrál]] nebo [[Kurzweilův integrál]]. | ||
| + | |||
| + | Nechť <big>\((X,\mathcal{A},\mu)\)</big> je [[Míra (matematika)|prostor s mírou]], pak pro [[měřitelná funkce|měřitelnou]] funkci <big>\(f:M \rightarrow \overline{\mathbb{R}}\)</big> definujeme '''horní''' Lebesgueův integrál: | ||
| + | |||
| + | :<big>\(\int\limits_\overline{M} f \ \mbox{d}\mu = \inf \sum\limits_{j=1}^{\infty} a_j \ \mu(A_j)\)</big>, | ||
| + | |||
| + | kde <big>\(\mathcal{A}\)</big> je <big>\(\sigma\)</big>-[[Sigma algebra|algebra]] na <big>\(X\)</big>, <big>\(A_{j} \in \mathcal{A}\)</big> jsou měřitelné množiny a | ||
| + | <big>\(M=\bigcup\limits_{j=1}^{\infty}A_j \in \mathcal{A}\)</big>, při <big>\(A_i \cap A_j = \emptyset\)</big> pro každé <big>\(i \neq j\)</big> a <big>\(a_j\geq f(x)\)</big> pro každé <big>\(x \in A_j\)</big>. | ||
| + | |||
| + | Nechť <big>\((X,\mathcal{A},\mu)\)</big> je [[Míra (matematika)|prostor s mírou]], pak pro [[měřitelná funkce|měřitelnou]] funkci <big>\(f:M \rightarrow \overline{\mathbb{R}}\)</big> definujeme '''dolní''' Lebesgueův integrál: | ||
| + | |||
| + | :<big>\(\int\limits_\underline{M} f \ \mbox{d}\mu = \sup \sum\limits_{j=1}^{\infty} a_j \ \mu(A_j)\)</big>, | ||
| + | |||
| + | kde <big>\(\mathcal{A}\)</big> je <big>\(\sigma\)</big>-[[Sigma algebra|algebra]] na <big>\(X\)</big>, <big>\(A_{j} \in \mathcal{A}\)</big> jsou měřitelné množiny a | ||
| + | <big>\(M=\bigcup\limits_{j=1}^{\infty}A_j \in \mathcal{A}\)</big>, při <big>\(A_i \cap A_j = \emptyset\)</big> pro každé <big>\(i \neq j\)</big> a <big>\(a_j\leq f(x)\)</big> pro každé <big>\(x \in A_j\)</big>. | ||
| + | |||
| + | '''Lebesgueův integrál''' pak definujeme pro funkci <big>\(f\)</big> splňující rovnost horního a dolního Lebesgueova integrálu jako: | ||
| + | |||
| + | :<big>\(\int\limits_M f \ \mbox{d}\mu = \int\limits_\overline{M} f \ \mbox{d}\mu = \int\limits_\underline{M} f \ \mbox{d}\mu\)</big>. | ||
| + | |||
| + | pozn.: Množina <big>\(\overline{\mathbb{R}}\)</big> je množina <big>\({\mathbb{R}}\)</big> rozšířená o <big>\(\pm \infty\)</big> a množina <big>\(X\)</big> může být např. [[Eukleidovský prostor|Euklidovský prostor]] <big>\({\mathbb{R}^n}\)</big>. | ||
| + | |||
| + | Lebesgueův integrál lze přibližně interpretovat jako nekonečný součet nekonečně úzkých pásů o "šířce" dané koeficientem <big>\(a_j \geq 0\)</big> a délce dané mírou množiny <big>\(\mu(A_j)\)</big> přes všechna <big>\(j \in \mathbb{N}\)</big>. | ||
| + | |||
| + | == Vlastnosti == | ||
| + | Pro některé funkce integrál nemusí existovat (například Newtonův nebo Riemannův integrál z [[Dirichletova funkce|Dirichletovy funkce]]), nebo může být nekonečný, např.: | ||
| + | |||
| + | :<big>\(\int\limits_0^1\frac{1}{x}\, \mathrm{d}x \,=\, +\infty\)</big>. | ||
| + | |||
| + | === Záměna sumy a integrálu === | ||
| + | Je-li dána [[řada (matematika)|řada]] [[funkce (matematika)|funkcí]] <big>\(\displaystyle f_n(x)\)</big> [[Spojitá funkce|spojitých]] na [[interval (matematika)|intervalu]] <big>\(\langle a,b\rangle\)</big> a pokud suma <big>\(\sum_{n=1}^\infty f_n(x)\)</big> [[stejnoměrná konvergence|konverguje stejnoměrně]], pak lze zaměnit sumu s integrálem: | ||
| + | |||
| + | :<big>\(\sum_{n=1}^\infty{\int\limits_a^b{f_n(x)\,\mathrm{d}x}}=\int\limits_a^b{\sum_{n=1}^\infty{f_n(x)}\,\mathrm{d}x}\)</big>. | ||
| + | |||
| + | === Záměna limity a integrálu === | ||
| + | Je-li <big>\(\displaystyle f(a,x)\)</big> [[funkce (matematika)|funkce]] [[Spojitá funkce|spojitá]] na příslušných definičních oborech <big>\(\displaystyle a, x\)</big> a pokud má integrovatelnou majorantu <big>\(\displaystyle g(x)\)</big> takovou, že <big>\(\displaystyle |f(a,x)|< g(x)\)</big> pro dané hodnoty parametru <big>\(a\)</big>, pak pro <big>\(\int_M g(x)\,\mathrm{d}x<+\infty\)</big> lze zaměnit limitu s integrálem: | ||
| + | |||
| + | :<big>\(\lim_{a\to a_0}\int_M{f(a,x)\,\mathrm{d}x}=\int_M{\lim_{a\to a_0}f(a,x)\,\mathrm{d}x}\)</big>. | ||
| + | |||
| + | == Zobecnění == | ||
| + | === Nevlastní integrál === | ||
| + | {{Podrobně|Nevlastní integrál}} | ||
| + | === Křivkový integrál === | ||
| + | {{Podrobně|Křivkový integrál}} | ||
| + | Křivkový integrál je integrál [[Skalární pole|skalárního]] nebo [[Vektorové pole|vektorového]] pole počítaný podél [[Křivka|křivky]]. | ||
| + | === Plošný integrál === | ||
| + | {{Podrobně|Plošný integrál}} | ||
| + | Plošný integrál je integrál [[Skalární pole|skalárního]] nebo [[Vektorové pole|vektorového]] pole počítaný podél [[Křivka|křivky]] ohraničující nějakou [[Plocha|plochu]]. | ||
| + | |||
| + | === Vícerozměrný integrál === | ||
| + | Integraci funkce více proměnných probíhá vždy na určité oblasti <big>\(\displaystyle\Omega\)</big>. Je-li <big>\(\displaystyle f(x_1,x_2,...,x_n)\)</big> funkcí <big>\(\displaystyle n\)</big> nezávisle proměnných, pak její integrál na určité <big>\(\displaystyle n\)</big>-rozměrné oblasti <big>\(\displaystyle\Omega\)</big> označujeme jako <big>\(n\)</big>-rozměrný integrál, přičemž jej zapíšeme některým z následujících způsobů: | ||
| + | |||
| + | :<big>\({\iint\cdots\int}_{\Omega} f(x_1,x_2,\ldots,x_n)\,\mathrm{d}\Omega = {\iint\cdots\int}_{\Omega} f(x_1,x_2,\ldots,x_n)\,\mathrm{d}x_1 \mathrm{d}x_2 \cdots \mathrm{d}x_n = {\iint \cdots \int}_{\Omega} f(x_1,x_2,\ldots,x_n)\,\mathrm{d}^n x\)</big>. | ||
| + | |||
| + | Počet integračních znaků <big>\(\int\)</big> odpovídá počtu proměnných, přes které integrujeme. Je-li ze zápisu integrálu zjevné, že se jedná o vícerozměrný integrál, pak zapisujeme pouze jeden integrační znak: | ||
| + | |||
| + | :<big>\(\int_\Omega f(x_1,x_2,\ldots,x_n)\,\mathrm{d}\Omega \,\)</big>. | ||
| + | |||
| + | Vícerozměrné integrály se obvykle řeší převodem na vícenásobnou integraci pomocí [[Fubiniova věta|Fubiniovy věty]]. Mezi vícerozměrné integrály řadíme např. plošný a objemový integrál. | ||
| + | |||
| + | === Komplexní integrál === | ||
| + | V [[komplexní rovina|komplexní rovině]] se užívají [[křivkový integrál|křivkové integrály]]. Pokud tyto integrály probíhají po uzavřené [[křivka|křivce]] ležící v komplexní rovině, lze je vypočítat pomocí [[Reziduum (matematika)|reziduové věty]], [[Cauchyův vzorec|Cauchyova vzorce]] nebo [[Cauchyova–Goursatova věta|Cauchyovy věty]]. | ||
| + | |||
| + | == Aplikace == | ||
| + | {{Viz též|Aplikace integrálu}} | ||
| + | |||
| + | === Plocha pod křivkou === | ||
| + | [[Soubor:Integral as region under curve.png|thumb|250px|Integrál jako plocha pod křivkou.]] | ||
| + | Určitý integrál nezáporné [[Spojitá funkce|spojité]] [[funkce (matematika)|funkce]] <big>\(f\)</big> na [[interval (matematika)|intervalu]] <big>\(\langle a,b\rangle\)</big> je roven ploše obrazce omezeného přímkami <big>\(x=a\)</big>, <big>\(x=b\)</big>, osou <big>\(x\)</big> a křivkou definovanou [[Graf (funkce)|grafem funkce]] <big>\(f\)</big>. Formálněji řečeno, takový integrál je roven [[Míra (matematika)|míře]] množiny <big>\(S\)</big> definované jako: | ||
| + | |||
| + | :<big>\(S=\{(x,y) \in \mathbb{R}^2:a \leq x \leq b ,0 \leq y \leq f(x)\}\)</big> | ||
| + | |||
| + | Je-li funkce někde záporná, plocha nad křivkou se počítá záporně. | ||
| + | |||
| + | === Fyzikální význam === | ||
| + | Určitý integrál se využívá v řadě fyzikálních definic – například určitý integrál síly podle polohy je vykonaná práce, určitý integrál ze zrychlení je změna rychlosti, [[Gaussova věta|objemový integrál]] z hustoty je hmotnost tělesa apod. | ||
| + | |||
| + | ==== Příklad ==== | ||
| + | Určitý integrál z rychlosti podle času je roven změně polohy během časového úseku od <big>\(t_1\)</big> do <big>\(t_2\)</big>. Pokud polohu v závislosti na čase označíme <big>\(x(t)\)</big>, platí: | ||
| + | |||
| + | :::<big>\(x(t_2)-x(t1) = \int\limits_{t_1}^{t_2}v(t) \,\mathrm{d}t\)</big>, tento vzorec je zobecněním známého vztahu pro pohyb konstantní rychlostí: | ||
| + | |||
| + | :::<big>\(x(t_2)-x(t_1) = v\cdot (t_2-t_1)\)</big> neboli <big>\(\triangle x= v \cdot \triangle t\)</big>, vzorce se liší v tom, že první vzorec lze použít i pro pohyb proměnlivou rychlostí. | ||
| + | |||
| + | == Literatura == | ||
| + | * [[Karel Rektorys|Rektorys, K.]] a spol.: ''Přehled užité matematiky I.''. Prometheus, Praha, [[2003]], 7. vydání. ISBN: 80-7196-179-5 | ||
| + | == Související články == | ||
| + | * [[Primitivní funkce]] | ||
| + | * [[Diferenciální rovnice]] | ||
| + | * [[Integrální rovnice]] | ||
| + | * [[Numerická integrace]] | ||
| + | |||
| + | == Externí odkazy == | ||
| + | * [https://web.archive.org/web/20130325084513/http://integrals.wolfram.com/index.jsp Online výpočet integrálu] | ||
| + | |||
| + | |||
| + | {{Článek z Wikipedie}} | ||
[[Kategorie:Integrální počet]] | [[Kategorie:Integrální počet]] | ||
Aktuální verze z 26. 12. 2024, 20:38
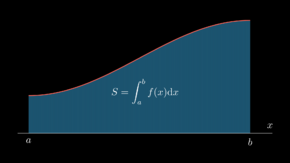
Určitý integrál je matematický nástroj, který umožňuje určit změnu funkce na základě informace o tom, jak rychle se funkce mění na daném intervalu. Určitý integrál nezáporné funkce má názornou geometrickou interpretaci, jedná se o obsah plochy pod grafem této funkce na uvažovaném intervalu.
Z formálního hlediska je vstupními údaji určitého integrálu funkce a dvě čísla (integrační meze) a výstupem je číslo (hodnota integrálu). Tím se liší od neurčitého integrálu, který má na vstupu funkci a výstupem je množina funkcí lišících se o aditivní konstantu.
Určitý integrál má mnoho aplikací v teorii pravděpodobnosti, funkcionální analýze, fyzice, např. častou fyzikální aplikací je určení dráhy tělesa ze známé rychlosti.
Obsah |
Definice
Existují různé definice určitého integrálu podle formulace integrálních součtů, tyto definice se liší množinou funkcí, které jsou podle nich integrovatelné (pokud je pro několik definicí funkce integrovatelná, pak je hodnota integrálu stejná), tj. existují různé určité integrály:
Newtonův integrál
Pokud je funkce \(f\) spojitá na intervalu \(\langle a,b\rangle\) a funkce \(F\) je k ní na tomto intervalu primitivní, pak platí:
- \(\int_a^b f(x) \ \mathrm{d}x = {[F(x)]}_a^b = F(b)-F(a)\).
Zobecněný Newtonův integrál
Newtonova definice určitého integrálu požaduje spojitost funkce na daném intervalu. Pokud je funkce na intervalu pouze po částech spojitá, lze interval v bodech nespojitosti rozdělit a hledat primitivní funkce po částech. Pro tento případ se definuje takzvaný „zobecněný Newtonův integrál“, který je v případě nespojitosti primitivní funkce v krajních bodech definován jako rozdíl jednostranných krajních limit:
- \(\int_a^b f(x) \ \mathrm{d}x = \lim_{x\to b^-} F(x)-\lim_{x\to a^+} F(x)\).
Riemannův integrál
Řekneme, že po částech spojitá funkce \(f\) na intervalu \(\langle a,b \rangle\) má Riemannův integrál \(I\), pokud pro každé \(\varepsilon > 0 \) existuje \(\delta>0\) takové, že pro každé dělení body \((D,C)\) intervalu \(\langle a,b \rangle\) platí, že:
- \(\lambda(D) < \delta \,=> \,|I - R(f,D,C)| < \varepsilon\), tj. \(I = \lim_{\lambda(D) \to 0}R(f,D,C) = \int\limits_{a}^{b} f(x) \ \mathrm{d}x\),
kde \(R(f,D,C)\) je Riemannova suma a \(\lambda(D)\) resp. \(C\) je norma dělení \(D\) resp. množina bodů zapouzdřených v dělení \(D\).
Lebesgueův integrál
Na základě Lebesgueovy míry definoval Henri Lebesgue tzv. Lebesgueův integrál. Má podobnou definici jako Darbouxova definice Riemannova integrálu, ale třída integrovatelných funkcí je v něm mnohem širší – dokonce se bez axiomu výběru nedá prokázat, že existuje funkce, která není Lebesgueovsky integrovatelná. Podobný postup použili i další matematici. Lebesgueův integrál a další, ještě pokročilejší integrály, umožňují integrovat širší třídy funkcí, platí pro ně silnější verze mnoha tvrzení a skýtají i mnoho jiných výhod. Patří mezi ně například Stieltjesův integrál nebo Kurzweilův integrál.
Nechť \((X,\mathcal{A},\mu)\) je prostor s mírou, pak pro měřitelnou funkci \(f:M \rightarrow \overline{\mathbb{R}}\) definujeme horní Lebesgueův integrál:
- \(\int\limits_\overline{M} f \ \mbox{d}\mu = \inf \sum\limits_{j=1}^{\infty} a_j \ \mu(A_j)\),
kde \(\mathcal{A}\) je \(\sigma\)-algebra na \(X\), \(A_{j} \in \mathcal{A}\) jsou měřitelné množiny a \(M=\bigcup\limits_{j=1}^{\infty}A_j \in \mathcal{A}\), při \(A_i \cap A_j = \emptyset\) pro každé \(i \neq j\) a \(a_j\geq f(x)\) pro každé \(x \in A_j\).
Nechť \((X,\mathcal{A},\mu)\) je prostor s mírou, pak pro měřitelnou funkci \(f:M \rightarrow \overline{\mathbb{R}}\) definujeme dolní Lebesgueův integrál:
- \(\int\limits_\underline{M} f \ \mbox{d}\mu = \sup \sum\limits_{j=1}^{\infty} a_j \ \mu(A_j)\),
kde \(\mathcal{A}\) je \(\sigma\)-algebra na \(X\), \(A_{j} \in \mathcal{A}\) jsou měřitelné množiny a \(M=\bigcup\limits_{j=1}^{\infty}A_j \in \mathcal{A}\), při \(A_i \cap A_j = \emptyset\) pro každé \(i \neq j\) a \(a_j\leq f(x)\) pro každé \(x \in A_j\).
Lebesgueův integrál pak definujeme pro funkci \(f\) splňující rovnost horního a dolního Lebesgueova integrálu jako:
- \(\int\limits_M f \ \mbox{d}\mu = \int\limits_\overline{M} f \ \mbox{d}\mu = \int\limits_\underline{M} f \ \mbox{d}\mu\).
pozn.: Množina \(\overline{\mathbb{R}}\) je množina \({\mathbb{R}}\) rozšířená o \(\pm \infty\) a množina \(X\) může být např. Euklidovský prostor \({\mathbb{R}^n}\).
Lebesgueův integrál lze přibližně interpretovat jako nekonečný součet nekonečně úzkých pásů o "šířce" dané koeficientem \(a_j \geq 0\) a délce dané mírou množiny \(\mu(A_j)\) přes všechna \(j \in \mathbb{N}\).
Vlastnosti
Pro některé funkce integrál nemusí existovat (například Newtonův nebo Riemannův integrál z Dirichletovy funkce), nebo může být nekonečný, např.:
- \(\int\limits_0^1\frac{1}{x}\, \mathrm{d}x \,=\, +\infty\).
Záměna sumy a integrálu
Je-li dána řada funkcí \(\displaystyle f_n(x)\) spojitých na intervalu \(\langle a,b\rangle\) a pokud suma \(\sum_{n=1}^\infty f_n(x)\) konverguje stejnoměrně, pak lze zaměnit sumu s integrálem:
- \(\sum_{n=1}^\infty{\int\limits_a^b{f_n(x)\,\mathrm{d}x}}=\int\limits_a^b{\sum_{n=1}^\infty{f_n(x)}\,\mathrm{d}x}\).
Záměna limity a integrálu
Je-li \(\displaystyle f(a,x)\) funkce spojitá na příslušných definičních oborech \(\displaystyle a, x\) a pokud má integrovatelnou majorantu \(\displaystyle g(x)\) takovou, že \(\displaystyle |f(a,x)|< g(x)\) pro dané hodnoty parametru \(a\), pak pro \(\int_M g(x)\,\mathrm{d}x<+\infty\) lze zaměnit limitu s integrálem:
- \(\lim_{a\to a_0}\int_M{f(a,x)\,\mathrm{d}x}=\int_M{\lim_{a\to a_0}f(a,x)\,\mathrm{d}x}\).
Zobecnění
Nevlastní integrál
- Podrobnější informace naleznete na stránce: Nevlastní integrál
Křivkový integrál
- Podrobnější informace naleznete na stránce: Křivkový integrál
Křivkový integrál je integrál skalárního nebo vektorového pole počítaný podél křivky.
Plošný integrál
- Podrobnější informace naleznete na stránce: Plošný integrál
Plošný integrál je integrál skalárního nebo vektorového pole počítaný podél křivky ohraničující nějakou plochu.
Vícerozměrný integrál
Integraci funkce více proměnných probíhá vždy na určité oblasti \(\displaystyle\Omega\). Je-li \(\displaystyle f(x_1,x_2,...,x_n)\) funkcí \(\displaystyle n\) nezávisle proměnných, pak její integrál na určité \(\displaystyle n\)-rozměrné oblasti \(\displaystyle\Omega\) označujeme jako \(n\)-rozměrný integrál, přičemž jej zapíšeme některým z následujících způsobů:
- \({\iint\cdots\int}_{\Omega} f(x_1,x_2,\ldots,x_n)\,\mathrm{d}\Omega = {\iint\cdots\int}_{\Omega} f(x_1,x_2,\ldots,x_n)\,\mathrm{d}x_1 \mathrm{d}x_2 \cdots \mathrm{d}x_n = {\iint \cdots \int}_{\Omega} f(x_1,x_2,\ldots,x_n)\,\mathrm{d}^n x\).
Počet integračních znaků \(\int\) odpovídá počtu proměnných, přes které integrujeme. Je-li ze zápisu integrálu zjevné, že se jedná o vícerozměrný integrál, pak zapisujeme pouze jeden integrační znak:
- \(\int_\Omega f(x_1,x_2,\ldots,x_n)\,\mathrm{d}\Omega \,\).
Vícerozměrné integrály se obvykle řeší převodem na vícenásobnou integraci pomocí Fubiniovy věty. Mezi vícerozměrné integrály řadíme např. plošný a objemový integrál.
Komplexní integrál
V komplexní rovině se užívají křivkové integrály. Pokud tyto integrály probíhají po uzavřené křivce ležící v komplexní rovině, lze je vypočítat pomocí reziduové věty, Cauchyova vzorce nebo Cauchyovy věty.
Aplikace
Plocha pod křivkou
Určitý integrál nezáporné spojité funkce \(f\) na intervalu \(\langle a,b\rangle\) je roven ploše obrazce omezeného přímkami \(x=a\), \(x=b\), osou \(x\) a křivkou definovanou grafem funkce \(f\). Formálněji řečeno, takový integrál je roven míře množiny \(S\) definované jako:
- \(S=\{(x,y) \in \mathbb{R}^2:a \leq x \leq b ,0 \leq y \leq f(x)\}\)
Je-li funkce někde záporná, plocha nad křivkou se počítá záporně.
Fyzikální význam
Určitý integrál se využívá v řadě fyzikálních definic – například určitý integrál síly podle polohy je vykonaná práce, určitý integrál ze zrychlení je změna rychlosti, objemový integrál z hustoty je hmotnost tělesa apod.
Příklad
Určitý integrál z rychlosti podle času je roven změně polohy během časového úseku od \(t_1\) do \(t_2\). Pokud polohu v závislosti na čase označíme \(x(t)\), platí:
- \(x(t_2)-x(t1) = \int\limits_{t_1}^{t_2}v(t) \,\mathrm{d}t\), tento vzorec je zobecněním známého vztahu pro pohyb konstantní rychlostí:
- \(x(t_2)-x(t_1) = v\cdot (t_2-t_1)\) neboli \(\triangle x= v \cdot \triangle t\), vzorce se liší v tom, že první vzorec lze použít i pro pohyb proměnlivou rychlostí.
Literatura
- Rektorys, K. a spol.: Přehled užité matematiky I.. Prometheus, Praha, 2003, 7. vydání. ISBN: 80-7196-179-5
Související články
Externí odkazy
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |